Правила
Новые идеи рассматриваются администрацией и могут быть приняты в разработку после обсуждения в Сенате, Конгрессе или ВМС.
Изменение системы расстояний., Труъ идея.
Итак, помнится мне уже писал я такие предложение в какой-то теме, месяца 4 назад, но найти не могу, потому, походу, прийдется с нуля писать.
Итак, для начала приведу текущее положение дел:
Минимальное расстояние 3000. Расстояние между планетами 50. Расстояние между системами 500. Расстояние между рукавами 2000.
Теперь что я предлагаю.
Во-первых - закольцевать рукава - расстояние из 1:1 в 1:999 сделать равным 500 (как между соседними системами) и т.п., думаю все поняли что я имею ввиду.
Выглядеть это будет так:
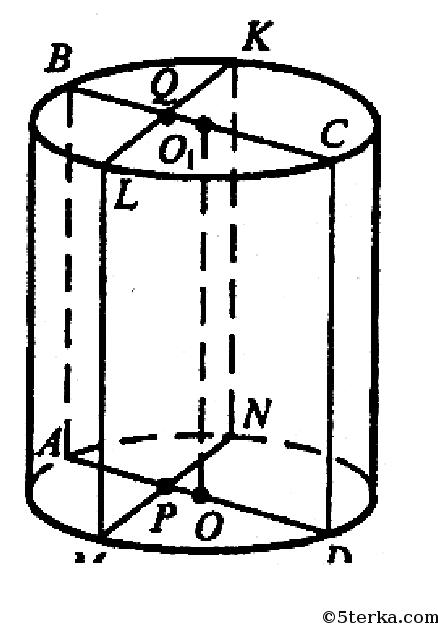
Пусть точка B - система 1:1 например, тогда точка K - примерно 1:200, точка С - 1:500, точка L - примерно 1:750. Точка A - 2:1, точка N - примерно 2:200 и т.д.. Кроме того, ОЧЕНЬ рядом с точкой B находится система 1:999 (а именно чуть ниже и левее, если смотреть на рисунок).
Это предложение довольно логично, и решит проблему очень большого расстояния между 1:100 и 1:900, например.
Во-вторых. Это самое интересное. Предлагаю сделать возможным пролетать не по линии окружности, то-есть пролетая все системы между системой отправления и системой назначения, а внутри окружности. На рисунке выше - имеется ввиду возможность перелета из L в K по прямой LK, или, например, из B в C по почти (почему почти, объясню позже) диаметру BC.
Основываться эта новая система расстояний будет на текущих. Как вы понимаете, для начала нужно рассчитать диаметр этой окружности. Включив мозг, мы понимаем, что для системы 1:1 диаметрально противоположной является "как-бы система" 1:500,5, а не 1:500, как можно было-бы подумать. Тогда расстояние до этой "как-бы системы" равно диаметру, который нам надо посчитать.
Итак. В текущей системе расстояний расстояние от 1:1 до 1:500,5 по линии окружности равно 499,5*500 = 249750. (Тут, кстати, еще заметим, для итоговой формулы, что длинна полуокружности - 499,5 расстояний между системами)
Из геометрических соображений диаметр данной окружности в пи/2 раз меньше расстояния по окружности, то-есть он составляет 249750/(пи/2) ~= 158995,788. Радиус равен половине диаметра: R = 158995,788/2 = 79497,894.
Данную величину (при вводе данной идеи, разумеется, можно данную величину округлить до 79500) будем считать "константой радиуса рукава". Все расчеты будут зависеть от нее, и, соответственно, при каком-либо изменении баланса будет писаться не "расстояние между системами уменьшено с 500 до 400", а "радиус рукава уменьшен с 79500 до 63600". Хотя для игроков, конечно, понятнее будет формулировка "уменьшен на 20%", которую и следует использовать.
Все, основная идея высказана, теперь займемся проблемой расчета расстояний между различными системами, для этого обратимся к формуле зависимости длинны хорды от центрального угла, опирающегося на эту хорду:
L=2* R * sin(a/2);
где L - искомое расстояние между системами (хорда окружности), R - радиус рукава, a - центральный угол, опирающийся на искомую хорду. Последнюю величину мы так-же не знаем, вот ее формула (обычные очевидные соображения):
a = ( пи / 499,5 ) * Δ;
где a - искомый угол, пи ~= 3,14, Δ - разница систем по линии окружности. Последняя величина требует пояснения, мне сложно объяснить ее смысл в теории, я воспользуюсь приведением примеров:
разница систем по линии окружности (далее Δ) от системы 1:1 до системы 1:5 равна 4;
Δ от системы 1:200 до системы 1:300 равна 100;
Δ от системы 1:1 до системы 1:500 равна 499...
И вот тут мы сталкиваемся с проблемой - ведь по первому пункту данной идеи Δ от системы 1:1 до системы 1:999 равна 1 (а до системы, например, 1:950, она равна 50). Для того, что-бы посчитать такую сложную переменную, нашим дорогим разработчикам придется ужас! сооружать в коде конструкцию вида if (?) then (...) else (...). Это, несомненно, непосильный труд, потому постараемся упростить предыдущие две формулы путем вложения второй в первую, авось что-нибудь прояснится:
L=2* R * sin( ( пи/499,5 ) * Δ/2);
L=2* R * sin( пи / (999/Δ) );
Итак, путем равносильных преобразований (Δ ≠ 0) мы пришли к выводу - аргументом синуса является отношение (пи) к (999/Δ). И что мы видим - из-за того, что функция синуса такая прекрасная зеркально ведет себя что при увеличении аргумента с 0 до (пи/2), что при уменьшении с (пи) до (пи/2), мы можем переменную Δ рассчитывать просто как модуль разности между системами! То-есть для нас вообще не важно Δ = 1 или Δ = 998, результат будет одинаков (так-же неважно, Δ = 949 или Δ = 50, и т.п.).
Итак, как мы поняли,
Δ = |S1 - S2|;
где S1 - система отправления, S2 - система назначения, | | - знак модуля.
И итоговая формула принимает вид:
L=2* R * sin( пи / (999/ |S1 - S2| ) );
Все!
Теперь обобщу - я предлагаю заменить текущую формулу расстояний между системами, которая выглядит так:
L = |S1 - S2| * 500;
на, по моему мнению, лучшую формулу:
L = 2* R * sin( пи / (999/ |S1 - S2| ) );
где R ~= 79500 (точнее 79497,894 , но лучше округлить при вводе, можно даже до 80000, там разница копеечная) .
Теперь немного графиков, они красиво показывают, зачем все это надо (на графике R ~= 79497,894):

Я еще раз подчеркну, что сильное различие в правой части графика обусловлено лишь закольцовыванием рукавов, а так разница, в действительности, не высока. Однако закольцовывание - несомненно нужное нововведение, этого баланс просто требует. Цель графика - дать понять, что кроме закольцовывания нужно и изменить формулу расстояний между системами (я замечу, что по-сути ВОООБЩЕ КОД МЕНЯТЬ НЕ НАДО. Просто в одном месте отредактировать формулу (как я себе представляю), может в 2-3 местах. Главная переменная (модуль разницы систем) остается той-же. R - не переменная, а константа.
Кроме того, график дает понять, что пока разница между системами отправления и назначения меньше 200 - разницы в расстоянии вообще особо не будет. Зато при полете в диаметрально противоположную точку рукава формула существенно (в (пи/2) ~= 1,57 раз) уменьшит расстояние, что очень логично.
В заключение хочу добавить, что, по моему мнению, если Вася тщательно вчитается в текст, он поймет что это нужная фишка. Она никак не повлияет на ближние полеты, зато позволит игрокам, находящимся далеко друг от друга (например новичек в 11:900 и его учитель в 7:100) плодотворно сотрудничать. Я верю и надеюсь, что идея будет введена а я получу медальку первого класса ^^ , много ведь текста накатал
Забыл добавить - расстояния в другие рукава будут как и раньше считаться по Пифагору, ничего нового.
И без флуда, позязя)
Upd: если ВДРУГ в текущем коде Δ = |S1 - S2| может быть равно нулю - можно перевернуть дробь внутри синуса, для того что-бы не возникала ошибка "деления на ноль". А именно для этого случая формула принимает вид:
L=2* R * sin( пи * |S1 - S2| / 999 );
тогда синус равен нулю, и разница систем, что логично, так-же равна нулю (при S1 = S2, я просто не знаю как у вас там в коде реализован рассчет расстояний).
Upd2: чуть подредактировал в одном месте, по-сути ничего не изменилось. (23:00 мск).
Upd3:
1) Я не против что-бы просто ввели закольцованность, не вводя второй пункт данной идеи!
2) И еще, тут были вопросы по поводу работы Алл.Сетей. Я, кажется, придумал как это реализовать.
Территория альянса будет представлять из себя сектора круга - центр сектора в центре рукава, а прямые, являющиеся границами сектора, приходят из центра рукава в границы Территории на окружности.
Масштабирование этой системы на цилиндр не сложно.
В рассчетах Алл.Сети ничего не изменится - просто "представлять" Алл.Сеть можно будет не как "территорию на 2-мерной поверхности" а как "набор секторов круга в 3-мерном пространстве". Очень красиво, если представить. И, кстати, очень логично выглядит. Да, вообще супер! Пойду Васе скину в личку, и добавлю в шапку.
Картинка:
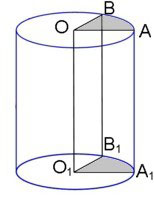
Тут сектор ABO - территория альянса в 1 галактике (то-есть на дуге AB все системы принадлежат альянсу), а сектор A1B1O1 - территория альянса во 2 галактике. Если во 2 галактике территория альянса меньше, то прямые AA1 и BB1 будут сужаться к плоскости 2 галактики. Красиво? Вроде очень. И логично же!
И трехмерная вселенная!
Upd4:
http://xcraft.ru/forum/topic_15520/4#post-412179 Хорошая картинка, объясняющая территорию Альянсовой Сети.
Итак, для начала приведу текущее положение дел:
Минимальное расстояние 3000. Расстояние между планетами 50. Расстояние между системами 500. Расстояние между рукавами 2000.
Теперь что я предлагаю.
Во-первых - закольцевать рукава - расстояние из 1:1 в 1:999 сделать равным 500 (как между соседними системами) и т.п., думаю все поняли что я имею ввиду.
Выглядеть это будет так:

Пусть точка B - система 1:1 например, тогда точка K - примерно 1:200, точка С - 1:500, точка L - примерно 1:750. Точка A - 2:1, точка N - примерно 2:200 и т.д.. Кроме того, ОЧЕНЬ рядом с точкой B находится система 1:999 (а именно чуть ниже и левее, если смотреть на рисунок).
Это предложение довольно логично, и решит проблему очень большого расстояния между 1:100 и 1:900, например.
Во-вторых. Это самое интересное. Предлагаю сделать возможным пролетать не по линии окружности, то-есть пролетая все системы между системой отправления и системой назначения, а внутри окружности. На рисунке выше - имеется ввиду возможность перелета из L в K по прямой LK, или, например, из B в C по почти (почему почти, объясню позже) диаметру BC.
Основываться эта новая система расстояний будет на текущих. Как вы понимаете, для начала нужно рассчитать диаметр этой окружности. Включив мозг, мы понимаем, что для системы 1:1 диаметрально противоположной является "как-бы система" 1:500,5, а не 1:500, как можно было-бы подумать. Тогда расстояние до этой "как-бы системы" равно диаметру, который нам надо посчитать.
Итак. В текущей системе расстояний расстояние от 1:1 до 1:500,5 по линии окружности равно 499,5*500 = 249750. (Тут, кстати, еще заметим, для итоговой формулы, что длинна полуокружности - 499,5 расстояний между системами)
Из геометрических соображений диаметр данной окружности в пи/2 раз меньше расстояния по окружности, то-есть он составляет 249750/(пи/2) ~= 158995,788. Радиус равен половине диаметра: R = 158995,788/2 = 79497,894.
Данную величину (при вводе данной идеи, разумеется, можно данную величину округлить до 79500) будем считать "константой радиуса рукава". Все расчеты будут зависеть от нее, и, соответственно, при каком-либо изменении баланса будет писаться не "расстояние между системами уменьшено с 500 до 400", а "радиус рукава уменьшен с 79500 до 63600". Хотя для игроков, конечно, понятнее будет формулировка "уменьшен на 20%", которую и следует использовать.
Все, основная идея высказана, теперь займемся проблемой расчета расстояний между различными системами, для этого обратимся к формуле зависимости длинны хорды от центрального угла, опирающегося на эту хорду:
L=2* R * sin(a/2);
где L - искомое расстояние между системами (хорда окружности), R - радиус рукава, a - центральный угол, опирающийся на искомую хорду. Последнюю величину мы так-же не знаем, вот ее формула (обычные очевидные соображения):
a = ( пи / 499,5 ) * Δ;
где a - искомый угол, пи ~= 3,14, Δ - разница систем по линии окружности. Последняя величина требует пояснения, мне сложно объяснить ее смысл в теории, я воспользуюсь приведением примеров:
разница систем по линии окружности (далее Δ) от системы 1:1 до системы 1:5 равна 4;
Δ от системы 1:200 до системы 1:300 равна 100;
Δ от системы 1:1 до системы 1:500 равна 499...
И вот тут мы сталкиваемся с проблемой - ведь по первому пункту данной идеи Δ от системы 1:1 до системы 1:999 равна 1 (а до системы, например, 1:950, она равна 50). Для того, что-бы посчитать такую сложную переменную, нашим дорогим разработчикам придется ужас! сооружать в коде конструкцию вида if (?) then (...) else (...). Это, несомненно, непосильный труд, потому постараемся упростить предыдущие две формулы путем вложения второй в первую, авось что-нибудь прояснится:
L=2* R * sin( ( пи/499,5 ) * Δ/2);
L=2* R * sin( пи / (999/Δ) );
Итак, путем равносильных преобразований (Δ ≠ 0) мы пришли к выводу - аргументом синуса является отношение (пи) к (999/Δ). И что мы видим - из-за того, что функция синуса такая прекрасная зеркально ведет себя что при увеличении аргумента с 0 до (пи/2), что при уменьшении с (пи) до (пи/2), мы можем переменную Δ рассчитывать просто как модуль разности между системами! То-есть для нас вообще не важно Δ = 1 или Δ = 998, результат будет одинаков (так-же неважно, Δ = 949 или Δ = 50, и т.п.).
Итак, как мы поняли,
Δ = |S1 - S2|;
где S1 - система отправления, S2 - система назначения, | | - знак модуля.
И итоговая формула принимает вид:
L=2* R * sin( пи / (999/ |S1 - S2| ) );
Все!
Теперь обобщу - я предлагаю заменить текущую формулу расстояний между системами, которая выглядит так:
L = |S1 - S2| * 500;
на, по моему мнению, лучшую формулу:
L = 2* R * sin( пи / (999/ |S1 - S2| ) );
где R ~= 79500 (точнее 79497,894 , но лучше округлить при вводе, можно даже до 80000, там разница копеечная) .
Теперь немного графиков, они красиво показывают, зачем все это надо (на графике R ~= 79497,894):

Я еще раз подчеркну, что сильное различие в правой части графика обусловлено лишь закольцовыванием рукавов, а так разница, в действительности, не высока. Однако закольцовывание - несомненно нужное нововведение, этого баланс просто требует. Цель графика - дать понять, что кроме закольцовывания нужно и изменить формулу расстояний между системами (я замечу, что по-сути ВОООБЩЕ КОД МЕНЯТЬ НЕ НАДО. Просто в одном месте отредактировать формулу (как я себе представляю), может в 2-3 местах. Главная переменная (модуль разницы систем) остается той-же. R - не переменная, а константа.
Кроме того, график дает понять, что пока разница между системами отправления и назначения меньше 200 - разницы в расстоянии вообще особо не будет. Зато при полете в диаметрально противоположную точку рукава формула существенно (в (пи/2) ~= 1,57 раз) уменьшит расстояние, что очень логично.
В заключение хочу добавить, что, по моему мнению, если Вася тщательно вчитается в текст, он поймет что это нужная фишка. Она никак не повлияет на ближние полеты, зато позволит игрокам, находящимся далеко друг от друга (например новичек в 11:900 и его учитель в 7:100) плодотворно сотрудничать. Я верю и надеюсь, что идея будет введена а я получу медальку первого класса ^^ , много ведь текста накатал
Забыл добавить - расстояния в другие рукава будут как и раньше считаться по Пифагору, ничего нового.
И без флуда, позязя)
Upd: если ВДРУГ в текущем коде Δ = |S1 - S2| может быть равно нулю - можно перевернуть дробь внутри синуса, для того что-бы не возникала ошибка "деления на ноль". А именно для этого случая формула принимает вид:
L=2* R * sin( пи * |S1 - S2| / 999 );
тогда синус равен нулю, и разница систем, что логично, так-же равна нулю (при S1 = S2, я просто не знаю как у вас там в коде реализован рассчет расстояний).
Upd2: чуть подредактировал в одном месте, по-сути ничего не изменилось. (23:00 мск).
Upd3:
1) Я не против что-бы просто ввели закольцованность, не вводя второй пункт данной идеи!
2) И еще, тут были вопросы по поводу работы Алл.Сетей. Я, кажется, придумал как это реализовать.
Территория альянса будет представлять из себя сектора круга - центр сектора в центре рукава, а прямые, являющиеся границами сектора, приходят из центра рукава в границы Территории на окружности.
Масштабирование этой системы на цилиндр не сложно.
В рассчетах Алл.Сети ничего не изменится - просто "представлять" Алл.Сеть можно будет не как "территорию на 2-мерной поверхности" а как "набор секторов круга в 3-мерном пространстве". Очень красиво, если представить. И, кстати, очень логично выглядит. Да, вообще супер! Пойду Васе скину в личку, и добавлю в шапку.
Картинка:

Тут сектор ABO - территория альянса в 1 галактике (то-есть на дуге AB все системы принадлежат альянсу), а сектор A1B1O1 - территория альянса во 2 галактике. Если во 2 галактике территория альянса меньше, то прямые AA1 и BB1 будут сужаться к плоскости 2 галактики. Красиво? Вроде очень. И логично же!
И трехмерная вселенная!
Upd4:
http://xcraft.ru/forum/topic_15520/4#post-412179 Хорошая картинка, объясняющая территорию Альянсовой Сети.
3 Июля 2014 22:48:58
блин я подобную идею вынашивал но чуть подругому, но все же так даже лучше, автору огромный +, админы обратите внимание на тему!!!!
4 Июля 2014 00:05:10
Это уже 3Д галактика получится, но кастрированная. Вы хотите чтоб сейчас это начали делать или сначала доделали старое и все что обещали еще месяц назад?
4 Июля 2014 00:08:33
Идея отличная, но вызывает опасение то что будет запилено как обычно коряво.
4 Июля 2014 00:20:09
Цитата: Raynor_Jim
Идея отличная, но вызывает опасение то что будет запилено как обычно коряво.
Джимми за это ты не переживай, проконтролируем. тут абсолютное большинство за эту идею, и к тому же Васин пас давно уже вскрыт нами...
4 Июля 2014 01:23:03
Какой то нуб подобное предлагал... Но суть всё же одна и та же - закольцевать это хорошо 
4 Июля 2014 05:45:23
4 Июля 2014 07:51:31
Цитата: MISHEL0
Во-первых - закольцевать рукава
Неплохо бы.
Цитата: MISHEL0
Во-вторых. Это самое интересное. Предлагаю сделать возможным пролетать не по линии окружности, то-есть пролетая все системы между системой отправления и системой назначения, а внутри окружности.
А ничего, что у нас пространство двумерное? С какого перепугу ты решил, что с поверхности цилиндра (т.е. нашей галактики при закольцованности рукавов) можно попасть на его противоположную точку сквозным путем? Уйдя в подпространство штоле?
4 Июля 2014 09:27:37
Цитата: человечина
Наша галактика не трехмерная
Это легко исправить.
Можно, конечно, долго говорить об отсутствии реалистичности, однако на данный момент у нас самая нереалистичная галактика - ну не бывает в галактике 100500кккк рукавов)
А вот мой вариант с цилиндрической галактикой, внутри которой можно летать, на мой взгляд довольно "реалистичен для нереалистичной вселенной" - по-крайней мере, такую систему можно представить в воображении без обращения к 4-му измерению. А вот текущую - Васину систему - без 4 измерения представить невозможно, да и с 4-м пока не особо понимаю как.
Цитата: человечина
А ничего, что у нас пространство двумерное?
Если представлять наше пространство как двумерное, то у него отсутствует ось вращения, что ставит его в крайне некрасивое положение. Я вообще не рассматриваю вариант представления нашей вселенной как двумерной.
Upd: "закругление" рукавов в реалистичной версии просмотра вселенной, когда 15 систем сразу показывает, вообще бредово выглядит без закольцовывания рукавов. В очень крайнем случае можно считать, что игровая вселенная - бесконечно большая галактика с бесконечно большим кол-вом рукавов, бесконечно закручивающихся. Однако в данном представлении пришлось бы считать, что в каждом рукаве бесконечное кол-во систем, иначе система не правдоподобна. А мы с Вами видим только 999 систем, противоречие...
И да, я не бред пишу в этом сообщении, если у Вас сложилось такое впечатление - прочитайте заново.
Upd2:
Цитата: человечина
С какого перепугу ты решил, что с поверхности цилиндра (т.е. нашей галактики при закольцованности рукавов) можно попасть на его противоположную точку сквозным путем?
О, я понял какую идею ты двигаешь! Да, красиво, может даже реалистично. Однако закольцованности рукавов это не меняет, плюс остается "острый угол на графике": если ввести закольцовывание, но не ввести пролет внутри цилиндра, красная линия на графике совершит резкий слом вниз в центре, и будет уродский угол. Хотя повторюсь, этот вариант так-же реалистичен, однако так-же требует закольцованности. Мне понравилось твое видение мира.
Upd3: И все-же, трехмерная система лучше двумерной - не так ли? Уже вижу вывеску на главной "Приглашаем Вас поиграть в онлайн стратегию с трехмерной вселенной!"
4 Июля 2014 20:30:04
MISHEL0, расстояния и время в вашей моделе лучше чем в нашей, но визуальное отображение территорий альянсов представляется мне слабо. А ведь ради этого всё и затевалось.
4 Июля 2014 22:07:01
Цитата: VasyaMalevich
но визуальное отображение территорий альянсов
ради этого вы превратили игру в какашку??? красаучег...
4 Июля 2014 22:13:47
Если выбирать:
- расстояние и время полетов
или же :
ТО , думаю бешенство крафта склонится к первому... чем к второму варианту.....
- расстояние и время полетов
или же :
Цитата: VasyaMalevich
визуальное отображение территорий альянсов
ТО , думаю бешенство крафта склонится к первому... чем к второму варианту.....
4 Июля 2014 22:14:25
И так в принципе Ал сети не работают так как следует!
По этому согласен первый вариант вернет КОСМИЧЕСКУЮ СТРАТЕГИЮ,а не ФЕРМУ(которая сейчас)
Интерес пропадает к игре!(форум держит)С надеждами на счастливый конец.
По этому согласен первый вариант вернет КОСМИЧЕСКУЮ СТРАТЕГИЮ,а не ФЕРМУ(которая сейчас)
Интерес пропадает к игре!(форум держит)С надеждами на счастливый конец.
4 Июля 2014 22:50:24
Цитата: zveroboy
Если выбирать:
- расстояние и время полетов
или же :
Цитата: VasyaMalevich
визуальное отображение территорий альянсов
ТО , думаю бешенство крафта склонится к первому... чем к второму варианту.....
- расстояние и время полетов
или же :
Цитата: VasyaMalevich
визуальное отображение территорий альянсов
ТО , думаю бешенство крафта склонится к первому... чем к второму варианту.....
Поддерживаю. Доработаете с Мишей потом альянсы.
4 Июля 2014 22:53:14
Цитата: VasyaMalevich
визуальное отображение территорий альянсов представляется мне слабо.
А что сложного? Отображение галактики останется таким как сейчас, просто после 1:999 системы будет идти 1:1 система. А не так как сейчас: 1:999, 1:999 и т.д.
4 Июля 2014 22:56:39
замечательная идея 
которая даст нам действительно бесконечный космос
а не такой как есть от стенки до стенки

сломаем стену
которая даст нам действительно бесконечный космос
а не такой как есть от стенки до стенки

сломаем стену
4 Июля 2014 23:04:04
VasyaMalevich
но визуальное отображение территорий альянсов представляется мне слабо. А ведь ради этого всё и затевалось.
но визуальное отображение территорий альянсов представляется мне слабо. А ведь ради этого всё и затевалось.
Vasya M,
приведите хотябы пару примеров, эпичных войн и движений, из за вашей затеи?
4 Июля 2014 23:04:24
«
· Новые идеи ·
»
Информация
Вы не авторизованы
1 чел. читают эту тему (гостей: 1)
Пользователей: 0 Claude Bot